انجمن راسخون

haj114

کاربر طلایی1

تاریخ عضویت : آبان 1391

تعداد پست ها : 3991

تعاریف

تابع f روی مجموعه باز D در خط حقیقی، تحلیلی حقیقی است اگر برای هر x_۰ در D بتوان نوشت:

$f(x)=\sum_{n=0}^\infty a_n \left( x-x_0 \right)^n$

$= a_0 + a_1 (x-x_0) + a_2 (x-x_0)^2 + a_3 (x-x_0)^3 + \cdots$

در این فرمول ضرایب a_۰، a_۱، ... اعداد حقیقی هستند و سری برای x در یک همسایگی از x_۰ همگرا است. به صورت دیگر، یک تابع تحلیلی یک تابع بینهایت بار مشتق پذیراست به این صورت که سری تیلور در هر نقطه x_۰ در دامنه‌اش

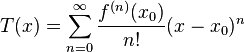
$T(x) = \sum_{n=0}^{\infin} \frac{f^{(n)}(x_0)}{n!} (x-x_0)^{n}$

برای x به اندازه کافی نزدیک به x_۰ همگراست و مقدارش برابر با f(x) است. تعریف یک تابع تحلیلی مختلط با جایگزین کردن «مختلط» به جای «حقیقی» و «صفحهٔ مختلط» به جای «خط حقیقی» در مطالب بالا بدست می‌آید.

* عَزیزٌ عَلَیَّ اَنْ اَرَی الْخَلْقَ وَلا تُری *

********

سه شنبه 5 شهریور 1392 6:20 PM