معادلات کوشی-ریمان

haj114

کاربر طلایی1

تاریخ عضویت : آبان 1391

تعداد پست ها : 3991

فرض کنید f(x + iy) = u + iv یک تابع از یک مجموعه باز از اعداد مختلط $\mathbb{C}$ به $\mathbb{C}$ باشد که در آن $x$ ، $y$ ، $u$ و $v$ حقیقی اند ( $u$ و $v$ توابع حقیقی-مقدار تعریف شده بر یک زیر مجموعه باز از $\mathbb{R}$ . آنگاه $f$ هلوموفیک است اگر و تنها اگر $u$ و $v$ به طور پیوسته مشتق پذیر باشند و مشتقات جزئی آنها در معادلات کوشی ریمان که

${ \partial u \over \partial x } = { \partial v \over \partial y }$

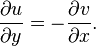
${ \partial u \over \partial y } = -{ \partial v \over \partial x } .$

هستند، صدق کنند. با یک فرمول بندی مختلط طبیعی، بینش هندسی بهتری بوجود می‌آید:

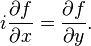
${ i { \partial f \over \partial x } } = { \partial f \over \partial y } .$

با توجه به معالات، اگر $u$ و $v$ دوبار مشتق پذیر باشند آنگاه مادامی که در معادلات لاپلاس صدق می‌کنند باید توابع همساز باشند. بنابراین معدلات می‌توانند به صورتی شرایطی بر روی یک جفت تابع همساز دیده شوند که بتوانند به عنوان بخش‌های حقیقی و موهومی یک تابع مختلط تحلیلی به کار روند. برای یک تابع داده شدهٔ همساز $u$ ، یک تابع همساز نظیر مانند $v$ ، یک همساز توأم نامیده می‌شود. اگر وجود داشته باشد، حداکثر یا یک عبارت ثابت منحصر بفرد است.

شکل دیگر معادلات کوشی-ریمان

فرض کنید 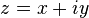$z = x + iy$ برای متغیرهای حقیقی x و y. آنگاه می‌توانیم بنویسیم $x = (z + \bar z)/2$ و $y = (z - \bar z)/(2i)$ . اکنون x و y توابع حقیقی از متغیرهای مستقل مختلط $\mathit{z}$ و $\bar z$ هستند. با مشتقگیری از x و y:

${\partial x \over \partial z} = {1 \over 2}\ \mathrm{and}\ {\partial y \over \partial z} = {1 \over 2i}$

همینطور

${\partial x \over \partial \bar z} = {1 \over 2}\ \mathrm{and}\ {\partial y \over \partial \bar z} = -{1 \over 2i}.$

با مشتقگیری از تابع $f (x, y) = u(x, y)+iv(x, y)$ داریم:

${\partial f \over \partial z} = {\partial f \over \partial x}{\partial x \over \partial z} + {\partial f \over \partial y}{\partial y \over \partial z}\ \mathrm{and}\ {\partial f \over \partial \bar z} = {\partial f \over \partial x}{\partial x \over \partial \bar z} + {\partial f \over \partial y}{\partial y \over \partial \bar z}.$

نهایتا با جاگذاری:

${\partial f \over \partial z} = {1 \over 2}\left({\partial f \over \partial x} + {1 \over i}{\partial f \over \partial y}\right)\ \mathrm{and}\ {\partial f \over \partial \bar z} = {1 \over 2}\left({\partial f \over \partial x} - {1 \over i}{\partial f \over \partial y}\right).$

اگر قرار دهیم ${\partial f \over \partial \bar z} = 0$ ، آنگاه ${\partial f \over \partial x} = -i {\partial f \over \partial y}$ و بنابراین

${\partial u \over \partial x} + i{\partial v \over \partial x} = -i\left({\partial u \over \partial y} + i{\partial v \over \partial y}\right),$

که برابر با معادلات کوشی-ریمان است.

نمایش قطبی معادلات کوشی-ریمان

با در نظر کرقتن نمایش قطبی 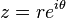$z=re^{i\theta}$ ، معادلات به این شکل در می‌آیند:

${ \partial u \over \partial r } = {1 \over r}{ \partial v \over \partial \theta},$

${ \partial v \over \partial r } = -{1 \over r}{ \partial u \over \partial \theta}.$

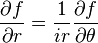
${\partial f \over \partial r} = {1 \over i r}{\partial f \over \partial \theta}$

که مشتقات روی $re^{i\theta}$ محاسبه شده اند.

* عَزیزٌ عَلَیَّ اَنْ اَرَی الْخَلْقَ وَلا تُری *

********

سه شنبه 5 شهریور 1392 6:06 PM