انجمن راسخون

haj114

کاربر طلایی1

تاریخ عضویت : آبان 1391

تعداد پست ها : 3991

مفهوم حد

مفهوم حد در ریاضی را می‌توان با این مثال توضیح داد: رشته عددهای ۱, ۱/۲, ۱/۴, ۱/۸,... اگر به همین حالت ادامه یابند همواره به صفر نزدیک‌تر می‌شوند ولی هیچ‌گاه به صفر نمی‌رسند بنابر این اصطلاحا می‌گوییم که صفر حَدّ این رشته عدد است.

به عبارتی، وقتی که مقادیر متوالی به یک متغیر نسبت داده می‌شود، و درنتیجه بی نهایت به عدد ثابتی نزدیک شوند، به طوری که اختلاف آنها از مقدار ثابت به هر اندازه کوچک قابل انتخاب باشد، این مقدار ثابت را حد همه مقادیر متغیر می‌گویند.

کاربرد مفهوم حد در ریاضی در توصیف مقداری است که یک تابع یا دنباله به آن نزدیک می‌شود، هنگامی که ورودی آن تابع یا شمارندهٔ آن دنباله به یک مقدار مشخص نزدیک می‌شود

. حد یک مفهوم اساسی در حساب دیفرانسیل و انتگرال و در حالت کلی در آنالیز ریاضی است و در تعریف پیوستگی، مشتق و انتگرال کاربرد دارد.

موضوع حد، به منظور بیان رفتار یک تابع می‌پردازد و می‌تواند رفتار آن را در نقاط روی صفحه و یا در بی نهایت هم ارزیابی کند.

مفهوم حد یک دنباله به حالت کلی تر حد شبکهٔ مکان‌شناسی گسترش می‌یابد و ارتباط نزدیکی با حد و حد مستقیم در نظریهٔ رده‌ها دارد.

ریاضی‌دانان پیش از آنکه مفهوم دقیق تر حد را ارائه کنند، در مورد آن مجادله‌های بسیار کرده‌اند. یونانی‌ها در عصر باستان درکی از مفهوم حد داشته‌اند. برای نمونه ارشمیدس مقدار تقریبی را با استفاده از پیرامون چند ضلعی‌های منتظم محاط در دایره به شعاع یک، وقتی که تعداد اضلاع بدون کران افزایش می‌یابد به دست می‌آورد. در قرون وسطی نیز تا دورهٔرنسانس مفهوم حد برای بدست آوردن مساحت شکل‌های گوناگون بکار گرفته می‌شد.

در نوشتار ریاضی حد را گاهی به صورت lim نمایش می‌دهند مانند lim(a_n) = a، گاهی با یک پیکان رو به راست (→) نمایش می‌دهند مانند: a_n → a و گاهی هم به فارسی حد می‌نویسند.

حد تابع

فرض کنید f(x)‎ تابعی حقیقی و c عددی حقیقی باشد. عبارت

$\lim_{x \to c}f(x) = L$

بدین معنا است که اگر x به‌اندازهٔ کافی به c نزدیک شود مقدار f(x)‎ به‌اندازهٔ دلخواه به $L$ نزدیک خواهد شد. رابطهٔ ریاضی بالا را چنین می‌خوانیم: «حد $f$ از $x$ هنگامی که $x$ به $c$ نزدیک می‌شود برابر $L$ است.»

کوشی در ۱۸۲۱ و به دنبال او کارل وایراشتراس تعریفی که در بالا برای حد داده شد را ریاضی وار بیان کردند، این تعریف در سدهٔ ۱۹ میلادی با نام «تعریف (ε, δ) حد» شناخته شد. آن‌ها در این تعریف از اپسیلون، ε، برای نشان دادن یک مقدار مثبت بسیار کوچک بهره بردند. هنگامی که « $f(x)$ به‌اندازهٔ دلخواه به $L$ نزدیک می‌شود» به این معنی است که مقدار $f(x)$ کم کم در بازهٔ $(L - ε, L + ε)$ جای می‌گیرد. با کمک قدر مطلق چنین می‌نویسیم: $f(x) - L| < ε$ $|$
عبارت «هنگامی که $x$ به‌اندازهٔ کافی به $c$ نزدیک می‌شود» به این معنی است که مقدارهای حقیقی از $x$ را در نظر داریم که فاصلهٔ آن‌ها از $c$ کمتر از عدد مثبت دلتا، δ باشد. یعنی $x$ عضو یکی از دو بازهٔ $(c - δ, c)$ یا $(c, c + δ)$ است، نوشتار ریاضی این عبارت چنین است: $۰ < |x - c| < δ$ . نامساوی نخست یعنی فاصلهٔ میان $c$ و $x$ بیشتر از صفر است و $x \neq c$ است در حالی که نامساوی دوم می‌گوید فاصلهٔ $x$ از $c$ کمتر از $δ$ است.

توجه داشته باشید که تعریف بالا برای حد می‌تواند درست باشد حتی اگر 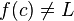$f(c) \neq L$ باشد. در حقیقت حتی نیازی نیست که $f(x)$ در $c$ تعریف شده باشد.

برای نمونه اگر داشته باشیم:

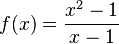
$f(x) = \frac{x^2 - 1}{x - 1}$

آنگاه f(1) تعریف نشده‌است (بخش بر صفر) حال هر چه $x$ به ۱ نزدیک می‌شود، $f(x)$ متناسب با آن نیز به ۲ نزدیک می‌شود:

f(۰٫۹)	f(۰٫۹۹)	f(۰٫۹۹۹)	f(۱٫۰)	f(۱٫۰۰۱)	f(۱٫۰۱)	f(۱.۱)
۱٫۹۰۰	۱٫۹۹۰	۱٫۹۹۹	⇒ تعریف نشده ⇐	۲٫۰۰۱	۲٫۰۱۰	۲٫۱۰۰

بنابراین، مقدار $f(x)$ به ۲ نزدیک می‌شود هرگاه بتوانیم $x$ را به‌اندازهٔ کافی به ۱ نزدیک کنیم.

به عبارت دیگر 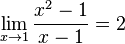$\lim_{x \to 1} \frac{x^2-1}{x-1} = 2$

یک تابع علاوه بر داشتن حد در مقدارهای معین، می‌تواند در بی نهایت هم دارای حد باشد. برای نمونه:

$f(x) = {2x-1 \over x}$

f(۱۰۰) = ۱٫۹۹۰۰
f(۱۰۰۰) = ۱٫۹۹۹۰
f(۱۰۰۰۰) = ۱٫۹۹۹۹۰

هرگاه $x$ مقدارهای بی نهایت بزرگ به خود گیرد، مقدار $f(x)$ به سوی ۲ کشیده می‌شود. در این حالت می‌گوییم حد $f(x)$ به ازای $x$ ‌های رو به بی نهایت، برابر ۲ است. بیان ریاضی این گفته چنین است:

گوییم $f(x)$ در نقطه‌ای مانند $x_0$ دارای حد $L$ است اگر به ازای هر عدد مثبت $\epsilon$ عدد مثبتی مثل $\delta$ موجود باشد به طوری که اگر $0 <|x-x_0| <\delta$ ، آنگاه $|f(x)-L| <\epsilon$ .

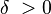به عبارت دیگر برای هر $\varepsilon\ >0$ یک $\delta\ >0$ وجود داشته باشد، که برای هر $x_0$ با خاصیت $|x-x_0|< \delta\$ ، داشته باشیم $|f(x)-L|< \varepsilon$ .

برای تعریف غیرصوری باید گفت حد تابع $f(x)$ ، $L$ است اگر وقتی $x \to a$ ، $f(x)$ به حد $L$ نزدیک بشود، یا $f(x)$ در $a$ دارای حد $L$ است، اگر هنگامی که $x$ به $a$ میل می‌کند، $f(x)$ به $L$ نزدیک شود.

مثال

اثبات $\lim_{x \to 0}\sqrt{x} = 0$ :

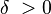برای هر $\varepsilon\ >0$ یک $\delta\ >0$ وجود دارد به شکلی که:

$|\sqrt{x}-0|< \varepsilon\$ اگر $0<x<\delta$

یا $\sqrt{x}< \varepsilon\$ اگر $0<x<\delta$

با گرفتن جذر هر دو سمت می‌توانیم عبارت قبلی را به شکل زیر بنوسیم:

$\sqrt{x}< \epsilon^2$ اگر $0<x<\delta$

بنا بر این $\delta \le \epsilon^2$

و این $\lim_{x \to 0}\sqrt{x} = 0$ را اثبات می‌کند.

حد یک دنباله

دنبالهٔ روبرو را در نظر بگیرید: ۱٫۷۹, ۱٫۷۹۹, ۱٫۷۹۹۹,... می‌توان دریافت که اعداد این دنباله به عدد ۱٫۸ نزدیک می‌شوند. ۱٫۸ حد این دنباله‌است.

فرض کنید a_۱, a_۲,... دنباله‌ای از عددهای حقیقی است. آنگاه می‌توان گفت عدد حقیقی $L$ حد این دنباله‌است هرگاه:

$\lim_{x \to \infty} \frac{2x-1}{x} = 2.$

اثبات

روش اثبات اپسیلون و دلتا مشهور است که بار اول توسط ریاضیدان آلمانی کارل ویستراس عنوان شد. با استفاده از آن حد را چنین تعریف می‌کنیم:

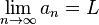
$\lim_{n \to \infty} a_n = L$

یعنی:

به ازای هر عدد حقیقی ε > ۰ می‌توان یک عدد طبیعی n_۰ پیدا کرد به گونه‌ای که برای تمام n > n_۰ آنگاه .

عبارت بالا بدان معنا است که همهٔ عضوهای دنباله به حد دنباله نزدیک می‌شوند چون عبارت قدر مطلقی برابر است با فاصلهٔ میان a_n و $L$ . همهٔ دنباله‌ها دارای حد نیستند، اگر دنباله‌های حد داشت به آن همگرا و اگر نداشت واگرا می‌گوییم. می‌توان نشان داد که دنباله‌های همگرا، حد یکتا دارند.

حد یک دنباله و حد یک تابع رابطهٔ نزدیکی با هم دارند.

* عَزیزٌ عَلَیَّ اَنْ اَرَی الْخَلْقَ وَلا تُری *

********

سه شنبه 5 شهریور 1392 4:58 PM