حلقه و میدان
سه شنبه 5 شهریور 1392 5:36 PM
حلقه
هرگاه  یک مجموعه ناتهی باشد ، گوییم مجموعه
یک مجموعه ناتهی باشد ، گوییم مجموعه  تحت دو عمل جمع و ضرب یک حلقه است ، هر گاه:
تحت دو عمل جمع و ضرب یک حلقه است ، هر گاه:
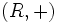 یک گروه جابجایی باشد
یک گروه جابجایی باشد یک نیمگروه باشد.
یک نیمگروه باشد. برقرار باشد.
برقرار باشد.
هرگاه حلقه  تحت عمل ضرب دارای خاصیت جابجایی باشد ، گوییم
تحت عمل ضرب دارای خاصیت جابجایی باشد ، گوییم  یک حلقه جابجایی(آبلی ) است.
یک حلقه جابجایی(آبلی ) است.
هرگاه  یک حلقه باشد ، عنصر
یک حلقه باشد ، عنصر  را یک مقسوم علیه صفر نامند ، هرگاه عضوی مانند
را یک مقسوم علیه صفر نامند ، هرگاه عضوی مانند 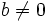 در حلقه
در حلقه  وجود داشته باشد ، بطوریکه
وجود داشته باشد ، بطوریکه .
.
در این تعریف اگر  ، آنگاه
، آنگاه 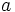 را مقسوم علیه چپ صفر مینامد و اگر
را مقسوم علیه چپ صفر مینامد و اگر  ،آنگاه
،آنگاه 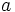 را مقسوم علیه راست صفر مینامند.
را مقسوم علیه راست صفر مینامند.
اگر  یک حلقه باشد،گوییم عنصری چون
یک حلقه باشد،گوییم عنصری چون  ،یک حلقه(واحد حلقه) است،هرگاه
،یک حلقه(واحد حلقه) است،هرگاه  تحت عمل ضرب، عضو همانی باشد. یعنی:
تحت عمل ضرب، عضو همانی باشد. یعنی:

اگر حلقه ای دارای عنصر واحد باشد، گوییم حلقه یکدار است و این یک را با نماد  نشان میدهیم.
نشان میدهیم.
حلقه ای که فقط شامل عنصر صفر باشد، حلقه بدیهی نامیده میشود.
اگر  ، حلقه بدیهی باشد، یعنی
، حلقه بدیهی باشد، یعنی 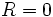 ، آنگاه
، آنگاه 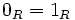 .
.
اگر  یک حلقه و
یک حلقه و  باشند ،آنگاه گزاره های زیر برقرارند:
باشند ،آنگاه گزاره های زیر برقرارند:
 1
1 2
2 3
3 4
4 5
5
هر گاه  یک حلقه یکدار باشد، عنصر
یک حلقه یکدار باشد، عنصر  را عنصر یکال مینامیم ، هرگاه
را عنصر یکال مینامیم ، هرگاه  دارای وارون ضربی باشد .یعنی:
دارای وارون ضربی باشد .یعنی:

 ، عنصر
، عنصر 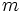 یکال است، هرگاه
یکال است، هرگاه 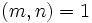 .
. یک حلقه مخالف صفرو
یک حلقه مخالف صفرو  یکدار نیز باشد، آنگاه
یکدار نیز باشد، آنگاه  .
. حلقه یکدار و
حلقه یکدار و  عنصر یکال باشد، آنگاه
عنصر یکال باشد، آنگاه 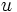 مقسوم علیه صفر نیست.
مقسوم علیه صفر نیست.
میدان
میدان در ریاضیات و جبر مجرد به معنای ساختاری جبری است که در آن چهار عمل جمع و تفریق و ضرب و تقسیم بجز تقسیم بر صفر تعریف شده باشد و هر دو عمل خاصیت جابجایی داشته باشند.
به بیان دیگر، میدان یک حلقه جابجایی است که اعضای غیر صفر آن تشکیل یک گروه بدهند.
اگر شرط جابجایی را برداریم، به جای میدان، حلقه تقسیم خواهیم داشت.
 ****
****