![]() ++C - بخش سوم
++C - بخش سوم
شنبه 28 فروردین 1389 9:34 AM
اسامي متغيرها، همانند
number1
،
number2
و
sum
مطابق با مكانهاي واقعي در حافظه كامپيوتر هستند. هر متغير داراي يك نام، نوع، سايز و مقدار است. در برنامه جمع
5-2
زمانيكه عبارت
زمانيكه مقداري در يك مكان حافظه قرار ميگيرد، مقدار جديد بر روي مقدار قبلي بازنويسي ميشود. مجدداٌ به سراغ برنامه جمع ميرويم، هنگامي كه عبارت
پس از اينكه برنامه مقادير
number1
و
number2
را بدست آورد، اين مقادير را با هم جمع كرده و مجموع را در درون متغير
sum
قرار ميدهد. عبارت

شكل 6-2 | مكان حافظه در حال نمايش نام و مقدار متغير
number1
.
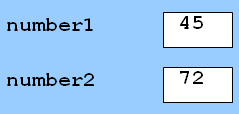
شكل 7-2 | مكانهاي حافظه پس از ذخيرهسازي مقادير براي
number1
و
number2
.

شكل 8-2| مكانهاي حافظه پس از محاسبه
sum
با استفاده از
number1
و
number2
.
6-2 محاسبات
اكثر برنامهها
محاسبات رياضي
انجام ميدهند
. عملگرهاي رياضي در جدول شكل
9-2
ليست شدهاند. توجه كنيد كه تمام نمادهاي بكار رفته در جبر در
C++
بكار گرفته نميشوند. علامت ستاره
(*)
نشاندهنده ضرب و
علامت درصد
(%)
نشاندهنده
باقيمانده
است
. اكثر عملگرهاي حسابي (در جدول
9-2
) از نوع عملگرهاي باينري هستند چرا كه هر عملگر
ما
بين دو عملوند قرار ميگيرد. براي مثال، عبارت حسابي
number1 + number2
شامل عملگر باينري
+
و دو عملوند
number1
و
number2
ميباشد.
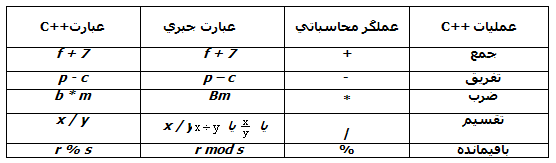
شكل 9-2 | عملگرهاي محاسباتي.
قوانين تقدم عملگر
C++
عملگرها را در عبارات محاسباتي با توالي كه قانون تقدم عملگرها تعيين ميكند بكار ميبرد. اين قوانين شبيه قوانين موجود در جبر هستند:
a((a + b) + C)
2- عملگرهاي ضرب و تقسيم
و باقيمانده
در مرحله بعدي بكار گرفته ميشوند. اگر عبارتي شامل چندين عملگر ضرب
،
تقسيم
و باقيمانده ب
اشد، عملگرها از سمت چپ به راست اجرا خواهند شد. ضرب
، ت
قسيم
و باقيمانده
داراي اولويت هم سطح يا برابر هستند.
3- عملگرهاي جمع و تفريق در آخرين مرحله به كار ميروند. اگر عبارتي شامل چندين عملگر تفريق و جمع باشد، عملگرها به ترتيب از سمت چپ به راست اجرا خواهند شد. عملگرهاي جمع و تفريق داراي اولويت هم سطح هستند.
وجود قوانين تقدم عملگرها
،
زبان
C++
قادر ميسازد تا عملگرها را با ترتيب صحيح بكار گيرد. در جدول شكل
10-2
خلاصهاي از قوانين تقدم عملگرها آورده شده است. اين جدول با معرفي عملگرهاي ديگر
C++
در فصلهاي بعدي تكميلتر خواهد شد. جدول كامل تقدم عملگرها در پيوست كتاب موجود است.
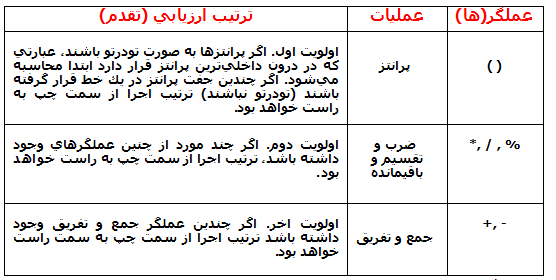
شكل 10-2 | تقدم عملگرهاي محاسباتي.
عبارات ساده جبري و
C++
حال اجازه دهيد تا به چند عبارت محاسباتي نگاهي بياندازيم تا بخوبي با قوانين تقدم عملگرهاي محاسباتي آشنا شويد. در هر مثالي كه ذكر ميشود عبارت جبري و معادل
C++
آن عبارت نيز آورده شده است. مثال زير يك عبارت رياضي را نشان ميدهد كه منظور از آن به دست آوردن ميانگين پنج عدد است:
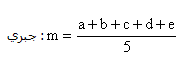
m = (a + b + c + d + e) / 5;: C++
عبارت زير نشاندهنده يك معادله است:
y = mx + b
y = m * x + b; : C++
مثالي كه در زير آورده شده حاوي عملگرهاي توان، ضرب، تقسيم اعشاري، جمع و تفريق است:
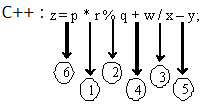
دايرههاي حاوي اعداد نشاندهنده ترتيب اجراي عملگرها هستند. عملگر
ضرب
در اولويت اول قرار دارد و عملگرهاي
باقيمانده
و تقسيم در اولويتهاي بعدي و به ترتيب از سمت چپ به راست اجرا ميشوند و پس از آنها عملگرهاي جمع و تفريق به ترتيب اجرا شده و در پايان عمل تخصيص صورت ميگيرد
.
توجه كنيد كه در اين جدول در مورد پرانتزهاي تودرتو مطالبي بيان شده است، اما تمام عبارات محاسباتي كه داراي چندين جفت پرانتز هستند، ممكن است حاوي پرانتزهاي تودرتو نباشد. براي مثال، اگر چه عبارت زير
a * (b + c) + c * (d + e)
شامل دو جفت پرانتز است، اما هيچ كداميك از آنها پرانتز تودرتو نميباشند. در چنين حالتي هر دو آنها داراي سطح يكسان ميباشند.
ارزيابي معادله درجه دوم
براي درك بهتر قوانين تقدم عملگرها به مثال زير كه يك چند جملهاي درجه دوم است توجه كنيد:
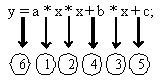
دايرههاي حاوي اعداد نشاندهنده ترتيب اجراي عملگرها هستند
.
در
C++
عملگر محاسباتي براي انجام عمل توان وجود ندارد، از اينرو عبارت
x2
را بصورت
x * x
نشان دادهايم. بزودي در مورد تابع استاندارد كتابخانهاي
pow
(توان) صحبت خواهيم كرد.
خطاي برنامهنويسي
برخي از زبانهاي برنامهنويسي از عملگرهاي
**
يا ^
براي نمايش توان استفاده ميكنند. در حاليكه زبان
C++
از اين عملگرها پشتيباني نميكند، و استفاده از آنها خطاي نحوي خواهد بود.
ح
ال فرض كنيد كه
a
،
b
،
c
و
x
بصورت
a = 2
،
b = 3
،
c = 7
و
x = 5
مقداردهي شده باشند. با توجه به شكل
11-2
تقدم عملگرها در اين چند جملهاي درجه دوم و نتيجه اجراي آنرا تعقيب ميكنيم.
برنامهنويسي ايدهال
در عمليات جبري استفاده از پرانتزهاي اضافي موجب ميشود كه عبارات از وضوح كافي برخوردار شوند (پرانتزهاي غيرضروري
redundant parentheses
يا پرانتزهاي افزونگي
نيز
نام
يده ميشوند
).
به كمك اين پرانتزها ميتوان عبارات بزرگ و پيچيده را دستهبندي كرده و سبب واضح شدن طريقه انجام محاسبات شد.