دروس نجوم اسلامی: مثلثات کروی

یکی از قدیمی ترین شاخه های دانش ستاره شناسی, نجوم کروی است. با عنایت به اینکه گفتیم برای حل بسیاری از مسایل ستاره شناسی, می توانیم تمام اجرام سماوی را روی یک کره فرضی بنام کره سماوی در نظر بگیریم, اهمیت نجوم کروی در محاسبات, روشن تر می شود. سابقه این رشته به 4000 سال پیش باز می گردد ولی هنوز در بسیاری از موارد نقش کلیدی را ایفا می کند.

دایره عظیمه

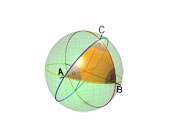
روی سطح یک کره می توان دوایر فرضی متعددی را در نظر گرفت. این دوایر به صورت نامحدود و با اندازه های مختلف قابل تصورند. به آن دسته از دوایری که مرکز آنها منطبق بر مرکز کره باشد, دایره عظیمه گفته می شود. پر واضح است از آنجا که شعاع دایره عظیمه مساوی شعاع کره است, محیط این دایره از تمام دوایر فرضی دیگر بزرگتر است و از اینرو نام آن را دایره عظیمه گذاشته اند.

کوتاه ترین فاصله بین دو نقطه واقع بر روی یک کره, قوس دایره عظیمه ای است که از آن دو نقطه عبور می نماید. این اصل هندسه کروی متناظر اصلی است که در هندسه مسطح برای کوتاهترین فاصله بین دو نقطه داریم, یعنی: کوتاهترین فاصله بین دو نقطه خط راستی است که از آن دو نقطه عبور می نماید. با توجه به این اصل در هندسه کروی, دید محاسباتی ما در بسیاری از مسایل مبتلی به، عوض می شود. یکی از مهمترین موارد استفاده از این اصل, محاسبه جهت قبله است. که در مقاله بعدی توضیح بیشتری در باره آن خواهیم داد.

مثلث کروی

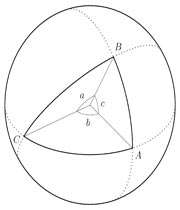
مثلث کروی مثلثی روی سطح کره است که هریک از اضلاع آن قوسی از دوایر عظیمه باشند. این مثلث از سه زاویه تشکیل می شود که معمولا با حروف بزرگ انگلیسی نمایش داده می شوند, مثلا می گوییم زوایای : A و B و C و دارای سه ضلع است که هرکدام کمانهایی از دوایر عظیمه هستند که معمولا با حروف کوچک انگلیسی نمایش داده می شوند, مثلا: کمانهای a و b و c .

مثلث کروی دارای خواصی متفاوت با مثلث مسطح است. از جمله:

مجموع سه زاوی یک مثلث کروی ممکن است از 180 درجه بیشتر باشد ولی از 270 درجه کمتر است.

اگر مجموع دو ضلع یک مثلث کروی برابر 180 درجه باشد, مجموع زوایای روبروی آنها نیز برابر 180 درجه خواهد بود.

در هر مثلث کروی اگر از مجموع شش ضلع و زاویه, سه عنصر معلوم باشد, می توانیم بقیه عناصر را نیز محاسبه نماییم. ریاضیدانان روابط زیادی بین عناصر یک مثلث کروی به اثبات رسانده اند. در اینجا به ذکر دو رابطه زیر بسنده می کنیم:

1- رابطه کسینوس:

در هر مثلث کروی، کسینوس هر کدام از اضلاع، برابر است با ضرب کسینوس دو ضلع دیگر بعلاوه ی ضرب سینوس همان اضلاع در کسینوس زاویه ی مقابل:

cos a = cos b cos c + sin b sin c cos A

cos b = cos a cos c + sin a sin c cos B

cos c = cos b cos a + sin b sin a cos C

2- فرمول های محاسبه نصف مجموع و یا تفاضل دو زاویه:

tan (A+B)/2 = (cos (a-b)/2 cot C/2 )/ cos (a+b)/2

tan (A-B)/2 = (sin (a-b)/2 cot C/2 )/ sin (a+b)/2

مثال:

برای سهولت درک روابط بالا یک مثال برای هریک از آنها می زنیم:

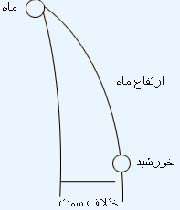
در شامگاه روز جمعه 17 دیماه 1378 مطابق با 29 رمضان 1420 , طبق استخراج برنامه نجوم اسلامی, بهنگام غروب آفتاب, تفاوت ارتفاع ماه و خورشید 6 درجه و اختلاف سمت آنها معادل 3 درجه بود. فاصله زاویه ای ماه و خورشید از دید ناظر زمینی چند درجه بود؟

در مثلث کروی که یک ضلع آن ارتفاع ماه و ضلع دیگر آن اختلاف سمت ماه و خورشید است, ضلع سوم نشان دهنده فاصله زاویه ای ماه و خورشید از دید ناظر زمینی است. چون ضلع ارتفاع بر دایره افق عمود است, داریم :

90 = A , با استفاده از فرمول کسینوس داریم:

cos a = cos b cos c + sin b sin c cos A

cos a = cos 6 cos 3 + sin 6 sin 3 cos 90 = cos 6 cos 3 = 0.9931

a = Arc cos 0.9931 = 6.70

بنابراین جدایی زاویه ای ماه و خورشید در آن لحظه، 70ر6 درجه بوده است.

تألیف:

دکتر محمد سمیعی

تنظیم برای تبیان:

ا.م.گمینی